標準偏差
標準偏差というのは,得点分布の「バラつき」のことである。たとえば100人が受験した平均50点のテストがある場合,全員が50点であることはまずないだろう。ある人は40点かもしれないし,ある人は60点かもしれない。こうしたデータのバラつきは,あらゆる統計的推測の基礎となるものであり,以降の説明でも繰り返し出てくることになるので,ここでは標準偏差の定義をしっかりと確認しておこう。
平均点が50点である同じテストでも,その得点の分布は図1のように異なったバラつきを持っている。テスト1 では35~65点の範囲にほぼ全ての得点が含まれるのに対し,テスト2では20~80,テスト3では0~100の範囲までにすべての得点が含まれている。こうした得点のバラつきを数値化するためにはどうすればいいだろうか。
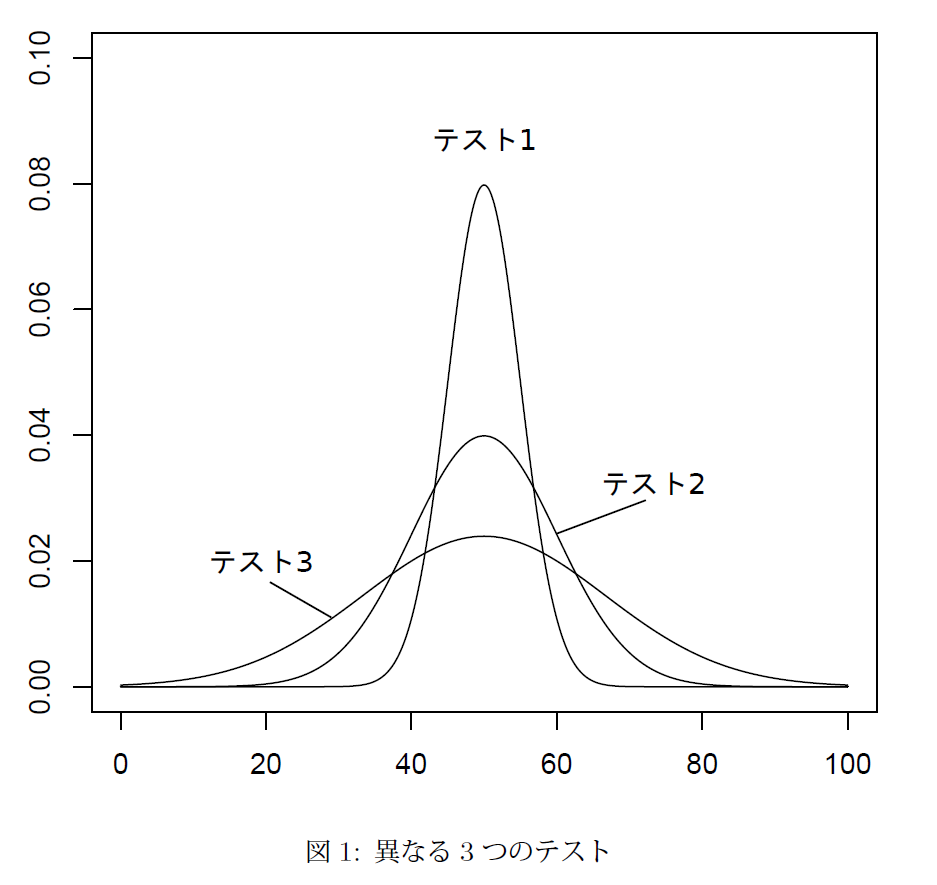
おそらく図1を見た人は,明らかにテスト1よりもテスト2が,テスト2よりもテスト3の方がバラつきが大きくなっていると直感的に判断するのではないだろうか。その判断の基準は,おそらく,平均値を軸とした分布の広がりであるはずだ。この平均からの差こそがバラつきの指標になるのである。
たとえば,平均が50点のテストに対する30点という得点は,平均値から20点のバラつきを持っているし,逆に70点の場合でも,平均値からは20点のバラつきを持っている。こうした個々の得点と平均値との差を「偏差」と呼ぶ。この偏差を使ってあるテストにおける得点分布のバラつきを表現したい。
しかし,ここで受験者の偏差を足し合わせていっただけでは,バラつきの指標にはならない。バラつきという概念に正負は関係ないからだ。30点も70点も平均値から20点バラついているというのは変わらない。しかし,個々の得点から平均を引くにせよ,或いはその逆にせよ,偏差を同じ式で計算すると,正の値と負の値で打消しあってしまう。そして平均の定義上,偏差の総計は必ず0 だ。
そこで,正負の符号を揃えるために,個々の偏差を2乗したものを足し合わせよう。たとえば,100人のテスト得点をそれぞれ,その平均得点を
とした場合,偏差を2乗したものの総和は,
と表現される。これは偏差平方和と呼ばれる。
しかし,偏差平方和だけではバラつきの指標にはならない。単純に受験者の数を増やすだけでその値が大きくなってしまうからだ。そこで偏差平方和の平均をとったもの
これが,分散と呼ばれるバラつきの指標になる。ただしnは受験者数である*1。しかし,分散は偏差の2乗を使っていたため,その単位も2乗になっている。また値も大きくなっているために,そのままでは直感的にデータのバラつきを把握しにくい。そこで,分散の平方根をとったもの
これが標準偏差(Standard Deviation)と呼ばれるものであり,あるデータセットのバラつきをあらわす指標となる。正規分布の場合,の範囲に約68%のデータが,
の範囲に約95%のデータが入る。また,
の範囲にはほぼ全てのデータが入ることがわかっている。
たとえば,図1のテスト2は平均50点,標準偏差10点の分布になっている。したがって,40~60点(±1SD)の範囲に全受験者の約68%が,30~70点(±2SD)の範囲に全受験者の95%が含まれ,20~80点(±3SD)の範囲にはほぼ全ての受験者が含まれている。
尺度の変換
次にデータの標準化を説明しよう。標準化とは,あるデータセットの尺度(スケール)を平均が0,標準偏差が1 となるように変換,調整する作業のことである*2。標準化を行うことで,それぞれのデータセットはお互いに比較することが可能なものとなる。
たとえば,図1のテスト1,2,3のそれぞれの標準偏差は,5点,10点,17点となっている。もし,今いずれかのテストで60点をとったとしても,テストの標準偏差が分からない限り10点という点差は単に平均点より上だったとしか解釈できない。また,テスト1ならば標準偏差を上回る成績だが,テスト3ならば標準偏差に満たない成績でしかない。そこで,個別のテストの尺度を共通の尺度で表現する必要性が出てくる。
それを説明する前に,正規分布の性質について,ここで一つ補足しておこう。
これは正規分布の確率密度関数である。確率密度という言葉が分かり辛ければ単に正規分布の関数だと思ってもかまわない。なおというのはネイピア数eのx乗という意味である。少し複雑な式に見えるかもしれないが,この式に使われている記号を確認してほしい。使われているのは,
,
,
,
,
の五つである。
このうちxは変数,また,円周率,ネイピア数
はそれぞれ値が決まっている定数である。そうすると,正規分布の関数形は平均
と標準偏差
(分散
)の二つによって決定されることがわかる。つまり,平均と標準偏差の二つさえわかってしまえば,ある1つの正規分布に特定できるということだ。
ここでデータの標準化に話を戻そう。データを標準化する,つまり複数のデータセットを同一の尺度上で表現するというのは,それぞれのデータセットの平均と標準偏差を揃えることを意味している。中でも平均が0,標準偏差が1の正規分布は標準正規分布と呼ばれ,この尺度上でデータを表現することを標準化と呼ぶのである。
まずは,式から示そう。平均が,標準偏差が
の正規分布に従うデータセット
]があるとき,
これが標準化変量と呼ばれるものになる。ただしi=1,2,…,nである。この作業によってデータセットXは標準正規分布上のデータとして扱うことができるようになった。このことは,平均と標準偏差の算出の仕方を思い出せば理解できるはずだ。
たとえば,データセットXの個々のデータそれぞれに一定の数
を加えるとどうなるだろうか。このとき,平均は
は
となり正規分布のグラフは
の分だけ平行移動する。偏差は
となり変化はないので分散,標準偏差の値は変わらない。なおカッコ内はその正規分布の平均点と分散である。

それではデータセットXに一定の数をかけた場合はどうなるだろうか。このとき,平均
は
となり正規分布のグラフは
だけ平行移動したあと
倍に「押しつぶされる」形となる。偏差は
となり
倍されるので分散は
倍,標準偏差は
倍となる。

倍したときには平均と標準偏差が同時に変化するため少しややこしく思えるかもしれないが難しく考える必要はない。要は「平均の変化はグラフの平行移動」,「標準偏差(分散)の変化はグラフの形状変化」と覚えておけばいい。
ここで(4)式に戻ろう。あるデータセットXからその平均点を引くというのは平均を0にする作業だ。この時点でXは平均0,標準偏差の正規分布に従っている。後はこのXに
を掛けてやれば,平均は0のまま,分散は
,標準偏差も1となる。
つまり,あるデータセットに対し平均を引いた後に標準偏差で割るという作業は,平均を0に,標準偏差(分散)を1のデータセットに変換する作業なのである。
もちろん尺度の変換は任意の尺度について可能である。たとえばあるテストの得点を平均が50,標準偏差10の尺度に変換したい場合,その得点を一旦標準化した後に10をかけて50を足してやればいい。つまりとなる。これがいわゆる偏差値と呼ばれるものだ。
また,尺度の変換は必ずしも一旦標準化する必要はない。尺度の変換とは要するにグラフの形を整えて位置を調整してやる作業である。たとえば二つのテストA,Bがそれぞれ平均,標準偏差
の正規分布に従っているとしよう。
このときテストBの得点をテストAの尺度上で表現したいならば,テストBの得点をとして
としてやればいい。やっていることは今までと何も変わらない。まず標準偏差の比を掛けることでテストAとテストBの形を同じにしてやる(第1項)。
後は平均点の差の分だけ平行移動してやれば二つのグラフは重なり合うことになるが,テストBの得点には標準偏差の比が掛けられているのでテストBの平均点はから
に変化している。したがってテストAとテストBの平均点の差は
(第2項)である。これを足してやれば二つのグラフは一致する。後述する「テストの等化」ではこの式に変形していた方がわかりやすい。
項目反応理論
項目反応理論(Item Response Theory=IRT)の概要は5章に示したが、概要だけで理解するというのは難しい。また以降の説明のためにも,もう少し詳細に説明をしておきたい。そこで,ここではIRTにおける確率モデルの導出,母数の推定,テストの等化という一連の作業を具体的に説明しておこう。
IRTでは受験者の潜在特性を推定すると述べたが,「学力」という目に見えない概念を何の仮定も置かずに推定することはできない。まずは「学力」」の分布を考えてみよう。経験的に考えれば学力というものは正規分布している可能性が高い。平均的な学力を有している人間が最も多く,そこから離れるに従って人数も減少していく。
そしてまた,ある母集団の学力分布が正規分布しているならば,その標本も正規分布に近似するはずだ。それでは,受験者集団の学力分布が正規分布していると仮定した場合,項目特性曲線(Item Characteristic Curve=ICC)はどのように描けるだろうか。
5章で示したICCの縦軸は正答確率となっていた。しかしこの正答確率という概念はいまいち把握しにくい。たとえば,受験者の潜在特性が正規分布していると仮定して,ある問題を与えた場合,一定の能力値以上の人間はほとんど解けるだろうし,一定の能力値以下の人間はほとんど解けないように思える。
しかし,測定というものに誤差はつきものである。実は,受験者の能力とその測定誤差が正規分布しているとき,ある受験者集団のある問題に対する正答割合,すなわち正答確率のモデルは正規分布の累積分布関数になることが導ける。累積分布関数とは簡単に言えば,正規分布の度数を累積的に積み上げていく関数である*3
そこで,IRTでは累積分布関数をICCとして利用する。先述したように尺度は任意に定めることができるので,ここでは平均0,標準偏差1の標準正規分布の累積分布関数を利用する。つまり,標準正規分布の密度関数を
としたとき,その累積分布関数は実数を用いて
と書ける。これは図6のような曲線になる。仮にテスト項目に対する正答確率が受験者の潜在特性だけで決定されるならば,この曲線がICCということになる。

もちろん,テストは受験者の能力だけで決定されるわけではない。どのIRTモデルを採用にするにしろ,少なくとも項目の困難度が表現されていなければならない。そこでの関数として,定数
,困難度
を用いて
とする。ただしは項目jの項目困難度である。この
を(7)式の
の部分に配すると,
となり,これは正規累積モデルと呼ばれる。式からわかるように,項目が難しければ曲線は右に移動するし,易しければ左に移動する。ここで重要なのは,ある問題に対する正答確率が,()という「受験者の潜在特性と項目困難度の差」によってのみ表現されているということだ。
たとえばのときも,
のときもその正答確率は変わらない。また,受験者の潜在特性と困難度が一致するとき,その正答確率は必ず0になる。ここから困難度は「それを五分五分の確率で解ける受験者の能力」と定義することができる。困難度が1であるというのは,潜在特性が1の受験者が五分五分の確率で解けるような難しさであるということだ。そのため潜在特性と困難度の単位は一致し,直感的な解釈が可能となる。
また(8)式のaは曲線の傾きを決定するパラメータであり,識別力と呼ばれる。今は全てのICCに共通の定数aとしているが,これを項目jの識別力とすれば,項目ごとの傾きを表現することができる。たとえば,図7は困難度が同じである二つの項目のICCである。

どちらの項目も潜在特性が0となっているところで,その正答確率が0.5となっている。したがってどちらの項目も困難度は0である。しかしその傾きは異なっている。が0より小さくなっているところではa=1.0の項目よりもa=2.0の項目の方が正答確率が低く難しい問題となっている。一方で,
が0より大きいところではa=2.0の項目よりもa=1.0の項目の方が正答確率が低く難しい問題となっている。
このことは,たとえ話を使うと理解しやすい。例えば,サッカーのリフティングとPKの成功率を考えてみよう。リフティングを20回連続で成功させるという課題は,熟練者にとっては容易なものだが,初心者にとっては極めて難しい課題となる。一方,PKの場合はプロでも外すことがあるのに対し,初心者でもそれなりの確率で成功させることができる。こうした課題による性質をIRTでは項目識別力をつかって表現することができる。
ここで項目の困難度と識別力という二つのパラメータがあることを説明したが,IRTではもう一つ「当て推量」というパラメータも存在する。どんなテストであっても,受験者の能力が正確に解答に反映されることは稀である。解けるはずの問題が解けないこともあれば,逆に解けない問題にたまたま正解してしまうことがある。当て推量はこの「偶然の正解」を表現した項目母数である。
特に,多肢選択式の問題の場合,受験者の実力に関係なく偶然に正解してしまう可能性が多分にある。この場合,当て推量の目安は選択肢の数の逆数となる。四択問題ならば,大体1/4の確率で正解してしまうというわけである。ただし,選択肢の数の逆数というのはあくまで目安である。実際には,明らかに排除できる選択肢や,逆に受験者をよく「迷わす」ことのできる選択肢が含まれている場合,当て推量母数の値は変化する。
IRTのモデルでは基本的にこの三つの項目母数が使われるが,常に全ての項目母数が利用されるわけではない。使われる項目母数の数によってモデルの名前も変わる。項目困難度だけを利用するモデルを1母数モデル,困難度と識別力を使うモデルが2母数モデル,3つの項目母数全てを使うモデルを3母数モデルと呼ぶ。1母数モデルでは当て推量が0,識別力は定数として扱う(通常は1)。二母数モデルでは当て推量を0として扱う。PISAで使われているのは1母数モデル,TIMSSで使われているのは2母数モデル(問題によって3母数モデル)である。
しかし,PISAやTIMSSで使われているのは(9)式のような正規累積モデルではない。正規累積モデルはその中に積分を含んでいるため計算が煩雑になってしまう。そこでロジスティック分布の分布関数を利用した近似式
が用いられることが多い。ただしD=1.7であり,当て推量パラメータは使っていない。これをロジスティックモデルという。PISAで使われているのは1母数ロジスティックモデル(正確にはラッシュモデル),TIMSSで使われているのは2母数,或いは3母数ロジスティックモデルである。以下の説明ではこちらのロジスティックモデルを使う。また簡単のため特に,1母数ロジスティックモデル(1 parameter logistic model=1PLモデル)について説明する。
まずは,(10)式をもう少し整えておこう。正答を1,誤答を0とする確率変数をXを用いると,潜在特性の受験者が困難度
の問題に正答する確率は
と表現できる。これが二値問題の正答確率を表現する1PLモデルだ。ただし,は全項目に共通の定数である*4。
と
の値がわかっていれば,この関数に当てはめることで正答確率を得ることができる。
しかし,問題はそのと
の値をどのように得るかである。それが事前にわかっていればそもそもテストをする必要はない。今,手元にあるのは受験者の潜在特性でもなく,項目の困難度でもない。受験者のテストに対する反応(結果)だけである。ここから,どのようにして
と
の値を推定すればいいのだろうか。
最尤推定
まずはそのための準備である。今,任意の受験者の潜在特性を
,任意の項目
の困難度
と表現するとき,受験者
が項目
に正答する確率を
と表現する。ただしは受験者iの項目jに対する反応であり,正答のとき1を,誤答のとき0をとる確率変数である。また誤答する確率を
と表現する。(12)と(13)をまとめると,受験者がある問題
に正答する確率は
と表現できる。正答と誤答はそれぞれ1と0の二値をとるので,正答の場合はが1となり,誤答の場合は
が1となり,式から消えるからだ。
これで受験者が項目
に正答する確率を表現できた。しかし,これは個々の問題に対する正答確率なので,次は複数のテスト項目に対する同時確率を知りたい。同時確率とは異なる事象が同時に成立する確率のことである。
たとえば,[11000]という反応パタンが観測されたとき,それぞれのテスト項目の反応が観測される確率は,
,
,
...となるが,今知りたいのは[11000]というパタン全体が観測される確率である。
受験者に
個のテスト項目が与えられるとき,その反応ベクトル,困難度ベクトルをそれぞれ
とする。ここで受験者の
個の項目に対する反応が独立であるならば*5,反応ベクトル
が観察される確率は
と表現できる。複雑な式に見えるかもしれないが,やっていることは単純である。は,右側の式を
から
まで変化させたものを掛け合わせるという意味だ。つまり,それぞれのテスト項目に対する正答・誤答の確率を掛け合わせたものになる。
さらに,この式をN人の受験者全体の反応行列が観測される確率に拡張しよう。受験者全体の反応行列Xが観察される確率は
\begin{equation}
X = \left[
\begin{array}{cccc}
x_{11} & x_{12} & \ldots & x_{1n} \\
x_{21} & x_{22} & \ldots & x_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
x_{N1} & x_{N2} & \ldots & x_{Nn}
\end{array}
\right] \\\tag{19}
\end{equation}
として,
\begin{equation}
f(X|\theta,b)=\prod_{i=1}^N f(x_i|\theta_i,b)=\prod_{i=1}^N\prod_{j=1}^n f(x_{ij}|\theta_i,b_j)\tag{20}
\end{equation}
と表現できる。こちらもやっていることは(17)式と変わらない。(17)式で得られた受験者の反応パタンをN人分掛け合わせているだけである。これが,N人の受験者がn個の項目を解いたときに得られる反応パタンが観察される確率である。
ただし,この式においては,
が定数であり,
が変数となっている。しかし,現実に得られるのは受験者のテスト結果,つまり反応ベクトル
であり,知りたいのは受験者の潜在特性
,および困難度
である。
そこで(20)式について,,
を変数,
を定数とみなした
\begin{equation}
L(X|\theta,b)=f(X|\theta,b)\tag{21}
\end{equation}
を尤度関数とよぶ。この式について「最尤推定」と呼ばれる推定を行うことで潜在特性と困難度
の推定値を得ることができる。最尤推定というのはIRTだけではなく,統計学において一般に用いられる推定法であり,聞きなれない言葉かもしれないが,我々が日常生活において使っている推定法でもある。
たとえば,通常の6面サイコロと12面サイコロの二つが存在するとしよう。今,どちらかのサイコロを振ったとして,その結果が5であることが分かっている。このとき,6面サイコロから5が出る確率は6分の1,12面サイコロから5が出る確率は12分の1となる。
したがって,振られたサイコロがどちらであったのかを考えると,6面サイコロの方だと推定するのが合理的である。つまり,何らかの現象が観測されたとき,その現象を最も生じさせやすい原因を推定するのが最尤推定である。
IRTでは,ある反応パタンが観測されたとき,最も高い確率でその反応パタンを生じさせると
の組み合わせを見つけることが,最尤推定の実際となる。たとえば,ある4問のテストがあるとしよう。その項目困難度が4問全て0で,またそのテストについて[1100]という結果を残した受験者の潜在特性を
としたとき,尤度関数は図8のようになる。

図の通り,尤度関数は,ある一点をピークとする単峰性の分布となる。これは困難度と尤度の関係でも同じである。この一点を見つけることが最尤推定なのである。ただし,(20)式は積の連なりとなって最大化しにくいため,実際に推定する際には対数変換をした
\begin{equation}
\log L(X|\theta,b)=\sum_{i=1}^N \sum_{j=1}^n [x_{ij}\log p_j(\theta_i)+(1-x_{ij})\log q_j(\theta_i)]\tag{22}
\end{equation}
を最大化することになる。単調増加関数で変換した場合,もとの関数の大小関係は保存される。(20)式を最大化すると
は元の関数も最大化するということだ。これを対数尤度関数と呼び,
,
について偏微分した結果を0とおいた方程式を解くことで最大化する母数を得ることができる。
このとき,と
を同時に推定するため,この推定法は同時最尤推定法とよばれる。しかし同時最尤推定法には欠点があり,第一に,計算量が膨大なものとなる。仮に,項目母数が既にわかっている状態で最尤推定を行う場合,1元の連立方程式を受験者の数だけ解けばよい。
しかし,同時最尤推定法ではテスト項目の困難度も未知母数とするため,たとえば,200人の受験者が全部で50問のテストを解くとき,1母数モデルでは,未知母数の数が200-2+50(受験者母数が-2となるのは,基準化の制約による)となり,248元連立方程式を解くことになる。
第二に,通常の統計モデルではデータを増やすほど安定した母数の推定を行うことが可能となるが,IRTの同時最尤推定法では,受験者を追加すると,その分だけ未知数である受験者母数が増えてしまい推定値が安定しない。また同じように,項目を追加すると未知数である項目母数が増えて推定値が安定しないという性質がある(豊田 2002)。この性質は,大規模学力調査の実施を困難にする。
周辺最尤推定
そこで,IRTにおける母数の推定には,主に周辺最尤推定法と呼ばれる手法が用いられる。周辺最尤推定では受験者母数を尤度関数から消すことで,安定した推定値の計算が可能となる。まず,周辺化という考え方を説明しよう。
今,白玉と黒玉がそれぞれ異なる割合で含まれている三つの壺A,B,Cが存在するとしよう。ここから,ランダムに壺を選び,その中から一つの玉を取り出すという試行をする。また,それぞれの壺から黒玉が出てくる条件付き確率は
\begin{eqnarray*}
p(黒|A) & = & 0.4 \\
p(黒|B) & = & 0.5 \\
p(黒|C) & = & 0.6
\end{eqnarray*}
とする。今知りたいのは,壺の種類によらず黒玉が取り出される確率である。仮に壺の選ばれる確率が均等であるなら,黒玉が取り出される確率は,
\begin{equation*}
p(黒)=\cfrac{1}{3}(p(黒|A)+p(黒|B)+p(黒|C))=0.5
\end{equation*}
となる。或いは,壺が選ばれる確率が均等でないとき,たとえばA,B,Cが選ばれる確率が,それぞれ0.2,0.3,0.5となっているときは,
\begin{equation*}
p(黒)=\cfrac{1}{5}p(黒|A)+\cfrac{3}{10}p(黒|B)+\cfrac{1}{2}p(黒|C)=0.53
\end{equation*}
となる。
つまり,それぞれの壺から黒玉が取り出される条件付き確率に,その確率が選ばれる(=壺が選ばれる)確率をかけて,その総和をとったものが壺の種類を無視した「黒玉が取り出される」確率になる。これは,条件付き確率の加重平均をとっているのと同じだ。これを,周辺化による局外母数(興味の対象の外にある母数)の消去という。
ただし,この方法を使う場合,当然ながら局外母数の確率分布が既知でなければならない。IRTの周辺最尤推定では受験者の潜在特性を局外母数として消去したいわけだが,この確率分布として何が利用できるだろうか。
説明の最初の方で述べたように,受験者の学力というのは正規分布に従っている可能性が高い。加えて,学力は潜在特性であるため,平均と標準偏差は任意に定めることができる。そこで,平均を0,標準偏差を1とした標準正規分布を,受験者の潜在特性の確率分布関数として利用する。
そうすると,受験者の反応ベクトル
が観測される確率は
を標準正規分布の確率密度関数として,
\begin{eqnarray}
f(x_i|b)&=&\int_{-\infty}^\infty g(\theta) f(x_i|\theta,b) d\theta \nonumber\\
&=&\int_{-\infty}^\infty g(\theta) \prod_{j=1}^n f(x_{ij}|\theta,b_j) d\theta \nonumber\\
&=&\int_{-\infty}^\infty g(\theta) \prod_{j=1}^n p_j(\theta)^{x_{ij}} q_j(\theta)^{1-x_{ij}}d\theta\tag{23}
\end{eqnarray}
と表現できる。ただしは項目の困難度ベクトル,
は項目
の困難度である。受験者の潜在特性
は,興味の外にある積分変数となっているため,添え字はつけていない。
しかし,ここでは説明のため,潜在特性をごく小さい階級幅をとった離散変数
]として考えてみよう。ただし,Nは受験者の数ではなく,単に
の最大値につけた添え字である。範囲は
とでもしておこう。
この場合,受験者が項目
に正答する確率は
\begin{eqnarray}
f(x_i|b_j)&=&g(\theta_1)f(x_1|\theta_1,b_j) \nonumber\\
&+&g(\theta_2)f(x_2|\theta_2,b_j) \nonumber\\
&\vdots& \nonumber\\
&+&g(\theta_N)f(x_N|\theta_N,b_j)\tag{24}
\end{eqnarray}
と書くことができる。たとえば,今,あるテスト項目について正解,つまりという反応が得られたとしよう。このとき,
から
までの,それぞれの場合について正答する確率を計算する。たとえば,
のとき計算される正当確率は30%になるかもしれないし,
のとき計算される正答確率は50%になるかもしれない。この正答確率は,先ほどの壺のたとえ話でいえば,それぞれの壺において黒玉が取り出される条件付き確率と同じである。
後は,それらの正答確率に,それぞれの潜在特性の割合(確率)をかけて総和をとれば,受験者の存在特性を無視した確率モデルを得ることができる。もちろん,この潜在特性の割合は既知である確率分布(連続変数の場合は確率密度関数)から得られる。ただし,実際には受験者の潜在特性
は-∞から∞までの連続変数であるため,(23)式のような積分表記となるのである。
さらに,N人の受験者の反応行列Xが得られる確率は,個々の確率の積となり,
\begin{eqnarray}
f(X|b)&=&\prod_{i=1}^N f(x_i|b) \nonumber\\
&=&\prod_{i=1}^N \int_{-\infty}^\infty g(\theta) \prod_{j=1}^n p_j(\theta)^{x_{ij}} q_j(\theta)^{1-x_{ij}}d\theta \tag{25}
\end{eqnarray}
となる。この後は,同時最尤推定と同じである。つまり,反応ベクトルを定数,困難度
を変数としたものを周辺尤度関数と見なす。それに対数変換を施した対数周辺尤度関数を最大化するような困難度母数の値を推定することになる。
ただし,実際の推定では連立方程式を数値的に解いて解を求めることは難しい。そのため,項目母数の推定には挟み撃ち法やニュートン法などを利用した,解析的な推定が行われる(豊田 2002)。
この周辺対数尤度関数を最大化するような項目母数の値を得ることがIRTにおける項目母数の推定である。ただし,この時点で得られた項目母数や潜在特性は,そのままでは他の受験者集団の潜在特性や,他のテストの項目母数と直接比較することはできない。受験者の潜在特性分布として利用した「平均が0,標準偏差が1」という尺度は任意に定めたものである。
そのため,同じテストを複数の集団が受験し,その集団ごとに項目母数を推定しても,得られる値は集団ごとに異なっている。たとえば,より学力の高い集団が受験したテストの項目母数はより低く推定されるし,より学力の低い集団が受験したテストの項目母数はより高く推定されることになる。
このことは,他の推定方法についても同じである。繰り返しになるが,受験者の学力やテスト項目の難しさは構成概念である。それを数値化するには,何らかの尺度を与える必要がある。しかし,この尺度を一意に決定することはできない。その数字自体に絶対的な意味は存在しないからである。
そこで,二つのテスト結果を比較可能にするために,「等化」という作業が必要になる。等化には共通の受験者を使う共通受験者デザインと,テスト間に共通項目を設ける共通項目デザインが存在する。どちらのデザインも理屈は同じなので,ここでは大規模学力調査で一般に使われる共通項目デザインを説明しよう。
テストの等化
先述したように,IRTでは受験者の潜在特性と項目母数を分離して考えている。言い換えれば,IRTでは潜在特性と項目母数の(語弊はあるが)本質的な量を測定していることになる。したがって,ある共通の問題,或いは共通の受験者の母数に二通りの値が計算されたとするならば,その違いは単なる「見た目」の違いであり,本質的には同じものである。つまり,二通りの母数について,共通の尺度を与えることができれば,その値は一致するはずだ。これがIRTにおける等化の原理である。
等化の方法には決まった一つの方法があるわけではない。ここではまず,多くのIRT調査に使われている,代表的な等化法であるmean-sigma法を説明しよう。
IRTにおける等化は,確率モデルを変形させることなく,任意に尺度の変換が可能である性質を利用する。今,
,
を用いた尺度を
として
\begin{eqnarray}
\theta_{i}^{*}&=&k\theta_i+l \tag{26} \\
a_{j}^{*}&=&\cfrac{1}{k}a_{j} \tag{27} \\
b_{j}^{*}&=&kb_j+l \tag{28}
\end{eqnarray}
とおく。ただしは項目
の識別力である。これを2母数ロジスティックモデルに代入すると,
\begin{eqnarray}
p_j(\theta_{i}^{*})^*&=&\cfrac{1}{1+exp(-Da_{j}^*(\theta_{i}^*-b_{i}^*)} \nonumber\\
&=&\cfrac{1}{1+exp(-D\cfrac{1}{k}a_{j}(k\theta_i+l-k(b_j+l)))} \nonumber\\
&=&\cfrac{1}{1+exp(-Da_{j}(\theta_i-b_j))}=p_j(\theta_i)\tag{29}
\end{eqnarray}
となる。ここでを,全ての項目に共通の定数
と置き換えてやれば,1母数モデルの場合も同様の変形が可能となる。また
とすれば常に
となり,事実上識別力母数を扱う必要はなくなり,式から省略することができる。
つまり,共通の問題,或いは共通の受験者についての二通りの母数は,一方の母数を一次変換したものが,もう一方の母数になっていると考えることができるのである。このときのと
を等化係数と呼ぶ。
では,等化係数はどうやって得ることができるのだろうか。mean-sigma法ではその名の通り,平均と標準偏差を利用する。ある1組の母数は,片方がもう片方を一次変換したものとみなすことができる。ということは,二通りの母数の値を標準化した結果は一致するはずである。つまり,次のような関係が成り立っている。
この式を変形すると
となる。今,項目母数はと変換されていたのだから,等化係数
と
の推定値は
となる。やっていることは先に見た尺度の変換と変わらない。(31)式は(5)式と同じである。ただし,1母数モデルの場合は困難度の標準偏差は変わらないので(k=aとしてaを式から消しているので),平均困難度の移動だけで等化することができる。
等化係数を計算する方法は他にもある。mean-sigma法は困難度の平均値と標準偏差を利用したが,識別力と困難度の平均値から等化係数を計算することも可能である。識別力の平均値からは(27)式によっての値が分かるし,それを使って(28)式に当てはめれば
の値も分かる。
この等化方法は二つの平均値を使うのでmean-mean法という直截な名前が付けられている。mean-sigma法もmean-mean法も非常に簡単に等化係数を得ることができるので,多くのIRTを用いたテストで利用されている。PISA2000-2003ではmean-sigma法が,それ以降の調査ではmean-mean法によって等化されている。
なお,mean-mean法であるとは言っても,PISAではラッシュモデル(1母数モデル)が使われており,各項目の識別力は一定のため(27式で言えばとなるため),実質的に項目困難度の移動だけで等化することができる。
或いは,二つの曲線の差を最小にするような推定もできるのではないかと思われたかもしれない。もちろんできる。平均や標準偏差といったモーメントを使った計算ではなく,二つのテスト特性曲線(TCC,縦軸が正答確率の総和)の差を最小二乗法などにより最適化する手法が南風原(1980),Stocking and Lord(1983)などにより提案されている。
いずれの等化法にも共通することは,共通の受験者や共通の項目を手がかりに等化を行うということである。前者を共通受験者デザイン,後者を共通項目デザインと呼ぶ。特によく使われる手法が,共通項目を異なる受験者に与える共通項目非等質グループデザインである。PISAもTIMSSもこのデザインによって運用されている。
ただし,PISAではmean-mean法,TIMSSでは同時尺度調整法(concurrent caribration)という等化手法が使われている。同時尺度調整法というのは,二つのテストから別々に母数を推定するのではなく,一つにまとめて推定してしまうやり方である。
たとえば,TIMSS1999とTIMSS2003から別々に母数を推定してそれを等化するのではなく,二つの年度のデータを一まとめにして母数を推定するのである。各年度のTIMSSのraw dataに過去の年度のデータも含まれているのはそのためだ。同時尺度調整法の場合は原理的に等化係数を計算する必要はない。
有意性検定
有意性検定は仮説検定とも呼ばれるように,何らかの統計的仮説の真偽を検証するための手段である。統計的仮説には様々なものがあるが,畢竟,二つのデータ*6間に「差がある」か「差がないか」という仮説に帰着する。前者の仮説を対立仮説,後者の仮説を帰無仮説と呼ぶ。
ここで,単に差が「ある・ない」と表現したが,そもそも二つのデータが全く同じであるということは殆どない。異なる二つのデータには,その大きさはともかく,必ず何らかの「ずれ」が存在するはずである。
そこで,統計的検定では,そのずれを確率的に評価するという方法をとる。つまり,二つのデータ間のずれが偶然の「誤差」の範囲内におさまるのか,そうではないのかを確率的に評価するのである。後者の場合,統計学的にみて「有意差がある」と表現される。
誤差は大きく分ければ標本誤差と非標本誤差に分けることができる。標本誤差とは標本を抽出する際に確率的に発生する誤差であり,母集団の特徴を完全には反映していない標本集団を抽出することによる誤差である。
非標本誤差とは文字通り,標本誤差以外の誤差であり,たとえば,長さを測定するものさしが歪んでいたりすることによる誤差である。このうち,誤差の分布が理論的に予測でき,したがって検定に利用することができるのは標本誤差の方だ。
PISA2000とPISA2003のデータを例に有意性検定を説明してみよう。利用するのはそれぞれの調査における日本の読解力の平均得点である。PISA2000では,日本の読解力は522.2点,PISA2003では498.1点である。この点数は等化した後の点数なので,直接比較することができる。したがって,522.2-498.1=24.1がPISA2000とPISA2003の点数の差ということになる。この差が統計的に有意であるといえるのか,そうではないのかを判断するのが検定という作業である。
しかし,有意性検定では対立仮説を直接検証することはできない。なぜならば,対立仮説は無数に存在するからだ。たとえば,PISA2000とPISA2003の平均得点に「10点の差がある」というのも一つの対立仮説である。仮に検定の結果,その仮説が採択されるとしても,「実は15点の差がある」,「やっぱり20点の差だった」という対立仮説が次から次へと出てくることになる。
また,仮説が棄却されるにしても,「9点の差」ならばあったかもしれないし,それが棄却されたとしても,「8点の差」という仮説ならば採択されるかもしれない。その対立仮説に決定的な意味があるのでない限り,対立仮説を直接の検定対象とすることはできない。逆に言えば,この作業を繰り返していくと「棄却されない(対立)仮説の範囲」というものも表現できることになるが,それは後述しよう。
そこで,有意性検定では,帰無仮説を棄却することができるかどうかによって,統計的仮説の判定を行うことになる。つまり,帰無仮説が正しいと仮定した場合に,観測されたデータが従う理論的な分布を明らかにし,その分布と観測されたデータのずれを確率的に評価することで,帰無仮説を棄却するか,しないかが判断される。
このとき棄却の判断基準として任意に設定された確率を有意水準と呼び,慣例的に0.05が設定されることが多い。言葉だけでは少しわかりにくいので,実際に図で確認してみよう。
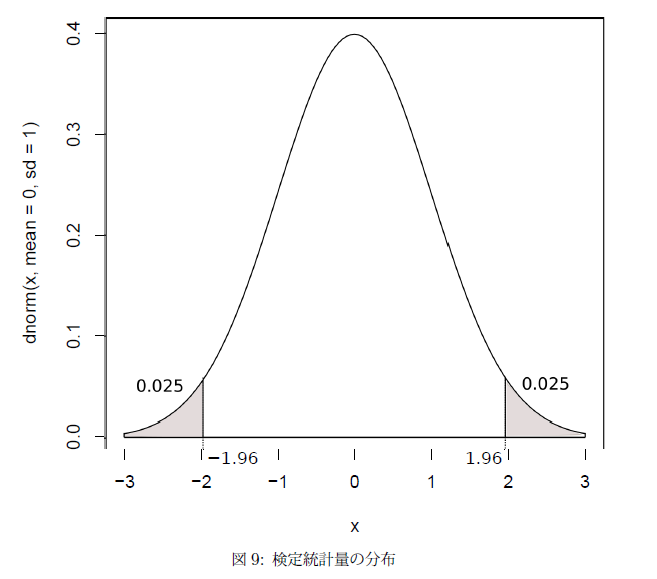
図9は,「帰無仮説が正しいと仮定した場合」の検定統計量が正規分布であった場合の確率分布である。検定統計量とは現実に観測されたデータを,検定がしやすいように加工したデータだと思えばいい。
たとえば,二つのテストの得点の差を標準化したものが検定統計量であり,その場合,図のように検定統計量は標準正規分布に従っている。設定した有意水準は0.05なので,両側検定の場合は両裾に0.025の棄却域が存在する。
もし,検定統計量がこの棄却域に入れば,それは,帰無仮説が正しいという仮定の下で,5%以下という非常に稀な確率でその事象が起こったことを意味する*7。このとき,帰無仮説は棄却され,対立仮説が採択される。正規分布の場合,両裾が0.025となるのはになる。標準正規分布の場合は
,
なので,そのまま±1.96の点となる。
PISA調査の例で言えば,「PISA2000とPISA2003の受験者の平均得点は同じ」というのが帰無仮説であり*8,24.1点という差が検定するべきデータになる。
つまり,PISA2000とPISA2003の受験者集団の平均得点に差はない,という仮定の下で,24.1点という差が確率的にどの程度稀であるのかによって帰無仮説を棄却するか否かを決定するのである。そしてそのためには,「二つの集団の平均点の差」という統計量が従う確率分布が明らかにされなければならない。
標本平均のバラつき
まずは,「テストの平均得点」のような標本平均が従う分布を明らかにしよう。たとえば今,日本人の平均身長が知りたいとしよう。そのために日本人から100人程度,無作為抽出したとする。このときの標本平均は168cmであった。ではこれをもう一度繰り返すとどうなるだろうか。
おそらく,その値は一回目の推定値とは異なっている。たとえば,170cmになっているかもしれない。さらに,もう一度同じ作業を繰り返してみよう。やはり,その値は一回目,二回目の推定値とは異なっているはずである。つまり,標本平均にもバラつきが存在するということである。
この標本平均のバラつきは,「中心極限定理」という統計学の定理を使えば,その理論的な分布を知ることができる。中心極限定理というのは母集団がどのような分布であっても,そこから抽出された標本平均の分布が正規分布するという定理である。つまり,日本人という母集団から100人を抽出して,その身長を平均した168cm,或いは170cmという値は正規分布に従っているのである。
今,中心極限定理により標本平均は正規分布に従っていることがわかっていた。そこで知りたいのは,この正規分布の平均と標準偏差(正確に言えばその不偏推定量)である。このうち,平均は簡単にわかる。たとえば,今,日本人の平均身長を調べるために,100人の標本集団の平均身長をその推定量としていた。この試行を無限に繰り返したときの標本平均の平均が,母平均に一致することは直感的に理解できるだろう。
一方,標準偏差がどうなるかといえば,これは母集団の標準偏差を標本サイズの平方根で割った値になる。つまり,標準偏差がの母集団から,サイズがnの標本を抽出すると,その標本平均の標準偏差は
になるのである。
また当然ながら,その分散は母集団の分散を標本サイズで割った値
になる。証明は長くなるので割愛するが,中心極限定理は統計学の基礎をなす定理であるので,その証明は多くの統計学の教科書に記載されている。
これで,標本平均が従う理論的な確率分布がわかった。標本平均の標準偏差は標準誤差(Standard Error)とも呼ばれる。つまり,標本平均と母平均との平均的な誤差のことである。たとえば,日本人の平均身長が170.0cm,その標準偏差が5.0cmだったとしよう。そうすると100人の標本集団の標本平均は,平均が170.0cm,標準偏差が=0.5となる。もし,日本人からランダムに100人を抽出すれば,その標本平均は平均的には0.5cm程度しかバラつかないということである。
少しわかりにくいかもしれないので,「標準誤差」という言葉の意味を説明しておこう。通常,母集団から抽出した標本を平均したものは母平均の推定値とみなされる。或いは逆に母平均を知りたいからこそ標本抽出は行われている。一つのデータから母平均を推定するよりも,複数のデータを平均した方がより精度の高い母平均の推定になることは経験的によく知られているからだ。
しかし,標本平均もまた標本と同様バラつきを持っている。そのバラつきは単なるバラつきではなく,母平均からの「誤差」である。身長が160cmの人と170cmの人が存在するのは単なる身長のバラつきだが,標本平均160cmと母平均170cmのずれは「推定値と真の値からのずれ」という意味で「誤差」なのである。これが標準偏差と標準誤差の意味の違いである。
平均点の差の検定
標本平均の分布は分かった。それでは,「平均点の差」はどういう分布に従っているのだろうか。実は,標本平均と同じように標本平均の差と和も正規分布に従うのである。しかも,その分散はそれぞれの標本平均の分散を足し合わせたものという非常に単純な式になるのである。図10は二つのテストの平均点の分布と,その差の分布である。

これでPISA調査について有意差を検定する準備が整った。まず,PISA2000とPISA2003の平均点を,それぞれ,
と表現すると,検定統計量は
となる。また,PISA2000とPISA2003の平均得点の標準誤差を,それぞれ,
とすると,検定統計量が従う分布の標準偏差は
となる。
さらに結果を分かりやすくするために,検定統計量を標準化しておこう。PISA2000とPISA2003の「真の」平均点(つまり母平均)をそれぞれ,
とすると,標準化された検定統計量は
となる。この統計量は標準正規分布に従うので,有意水準0.05に対応する境界点は±1.96となる
また,帰無仮説が正しいと仮定した場合は当然となる。したがって,次の不等式を満たすとき,帰無仮説は棄却されず,満たさないときは対立仮説が採択される。
\begin{equation}
-{1.96}\leqq \cfrac{(\bar{X}_{2000}-\bar{X}_{2003})}{\sqrt{SE_{2000}^2+SE_{2003}^2}} \leqq 1.96 \tag{34}
\end{equation}
それではこの式に実際のPISAのデータを当てはめてみよう。PISA2000とPISA2003の平均得点はそれぞれ,
,標準誤差は,PISAの報告書からそれぞれ,
,
であることがわかっている。
したがって,検定統計量はとなり,その結果は3.71である。したがって,PISA2000からPISA2003の間で見られた読解力の変化は「有意」であったということができるのである。
なお,(34)式は実際にPISAで使われている計算式ではない。TIMSSの場合はこの式で問題ないが,PISAの場合は標準誤差としてLinking Errorというものが加えられている。そのため,実際の検定統計量はもう少し小さくなる。
Linking Error
今説明したように,異なる年度間のPISAやTIMSSの得点が有意に変化しかどうかは,
の式を使えば判断することができる。しかし,PISA調査の場合は少し式を変えて次のような式が使われる。
\begin{equation}
-{1.96}\leqq \cfrac{(\bar{X}_{2000}-\bar{X}_{2003})}{\sqrt{SE_{2000}^2+SE_{2003}^2+Linking Error^2}} \leqq 1.96 \tag{36}
\end{equation}
見てわかるように,PISA調査における有意差の検定ではLinking Errorというものが分母の√の中に登場している。そのため,PISAでは通常の検定と比較して検定統計量が小さくなり,その分,帰無仮説を棄却する基準は厳しいものとなっている。
このLinking Errorとは一体何なのだろうか。まずは,表6.1を確認してほしい。
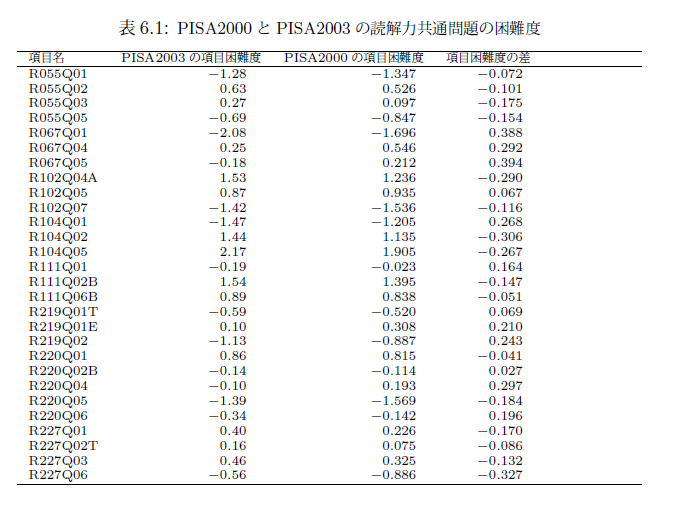
これはPISA2000とPISA2003の読解力問題における共通項目28問ついての表である。表には,PISA2000のデータのみから計算した項目の困難度と,PISA2003のデータのみから計算した項目の困難度,およびその差を載せてある。また,それぞれの項目困難度は28問の平均困難度が0になるように調整されている。
5章で(或いは先ほども)述べたように,ラッシュモデルの場合,同じ問題に対する二つの項目困難度は単に定数を加え合わせたものであった。したがって,二つの項目困難度を同じ尺度にのせるには,項目困難度をそれぞれの平均値を引いてやればいい。結果として,両者の項目困難度の平均は0になる。したがって,二つの項目困難度は等化されている。
しかし,両者の値は一致していない。これには二つの原因がありうる。一つは,上記の項目困難度は推定値であり,したがって「真の項目困難度」それ自体ではないということだ。既に見たように,推定の結果得られた母数の推定値は,テストの結果を最も有り得るように推定された値だ。推定値の結果が真の値と正確に一致することはほとんどない。そのため,テスト項目の情報を項目プールに追加するときなどは,二つの項目困難度の平均値が利用されたりする(豊田 2002)。また,この場合,受験者の数を増やしてやれば推定値は安定する。
しかし,ここで問題とするのは,もう一つの原因である。それは,IRTのモデルと現実のデータが適合していないことに起因している。項目反応理論は5章でも述べたように,項目困難度の不変性を前提している。困難度の不変性は,次の性質を満たすための十分条件となっている。
\begin{equation*}
\theta_{1} < \theta_{2} のとき,
P_{j}(\theta_{1}) < P_{j}(\theta_{2})
\end{equation*}
この性質は,異なる二つの能力を持つ受験者が同じ問題を解いたとき,それがどのような問題(逆転項目以外)であっても,能力が高いほうが,正答確率も高くなるということを意味している。この性質が学力調査において前提されることは自明であると言っていいだろう。困難度が不変であれば,この性質は常に満たされる。
しかし,現実のテスト場面ではこの性質が必ずしも成り立つわけではない。たとえば,テストには「位置効果」というものが知られている。これは,テストの最初の方に出された問題よりも,最後の方に出てくる問題の方が正答率が低くなってしまうという現象である。この場合,仮に同一の問題について,同一の能力を持つ受験者がそれを解いたとしても,問題がテストで出題される位置によってその困難度は変化してしまう。
これと同じようなことが,カリキュラムの変更によっても起こりうる。たとえば,カリキュラムの順番が変更されていれば,全体的な学力が同じ受験者であっても,より最近に学習した内容についての問題の方が正答率は高くなるだろう。あるいは,カリキュラムの範囲の変更によっても同様である。全体的な学力が同じ受験者であっても,カリキュラムの範囲,あるいはカリキュラムの重点によって,項目に対する反応には違いがでる。
項目困難度が変化するということは,等化係数が変化するということだ。等化係数が変化すれば最終的に推定される成績も変化する。たとえば単純な例を考えてみよう。図11を見てほしい。今5問で構成されたテストAを集団aが受験したとする。集団の潜在特性は全て等しく,また5問の困難度も全て等しく
だったとしよう。したがって集団aは全ての項目に対して平均正答率が50%となる。
しかし,現実には様々な要因によって正答率が変化することがある。たとえば,疲労によって正答確率が1問ごとに1%ずつ下がると仮定しよう。このとき項目1の正答確率は50%であり,項目5の46%まで1%ずつ下がることになる。
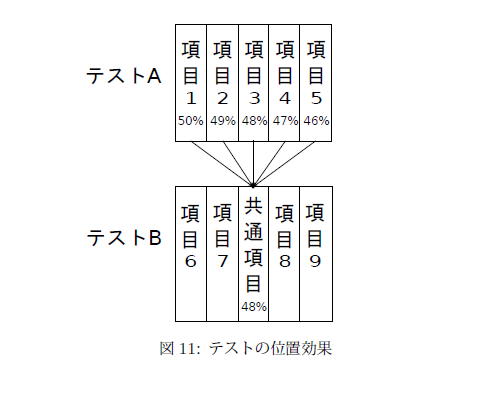
次に,集団aと全く同質の集団bにテストBを受験させる。テストBもテストAと同じく5問で構成されているが,二つのテストを等化するために,テストBの3問目には共通項目として項目1から項目5までのいずれかを出題することにする。また1問ごとに正答率が低下するのも集団aと同様だとしよう。
このとき項目1が共通項目として選ばれると,集団aの正答率が50%に対し集団bでは48%となってしまう。その分,集団aの能力は高く推定されることになる。一方で項目5が選ばれた場合,集団aの正答率が46%であるのに対し集団bでは48%となる。その分,集団aの能力は低く推定されることになる。
つまり「共通項目の選び方」によって推定結果が違うものになってしまうということだ。すなわちLinking Errorとは共通項目のサンプリング誤差なのである。そのため,いくら受験者の数を増やしたところで共通項目の数を増やさない限り,Linking Errorは小さくならない(Michaelides and Haertel 2004)。
また,受験者のサンプリングの際にその代表性に注意しなければならないのと同様に,共通項目のサンプリングもまた測定したい領域をできるだけ広くカバーするように出題されなければならない(Sheehan and Mislevy 1988)。
Linking Errorの計算
もし全ての有りうべき問題を共通項目として出題することができればLinking Errorは発生しない。しかし現実にはもちろんそんなことは不可能だ。それゆえPISAではLinking Errorを考慮した検定が行われるのである。それではLinking Errorはどう計算すればいいだろうか。
Linking Errorの計算には決まった手法があるわけではないが,PISA2003では困難度の差の標準誤差をそのままLinking Errorとして計算している。今,テストAの(共通)項目困難度を,テストBの(共通)項目困難度を
とする。ただし,これは推定値ではなく真の値である。そうすると,1母数モデルの場合,等化係数は
であり,また全ての
について
が成り立っている。
しかし,実際の困難度は推定値であるため真の値と一致するわけではない。また,先に説明したように項目困難度の性質が変化することによっても,推定値の値は変化する。
そこで,ここではテストAの結果にテストBの結果を等化させるとして,テストB側の困難度の変化をとしよう。ただし,
は平均0の正規分布に従う。つまり,誤差であると言うことだ。そうすると,実際に得られるテストBの困難度は
と表現される。したがって,その等化係数も
と変化する。
今知りたいのは,このの影響の大きさである。つまり,共通項目の数によって
がどれだけバラつくのかを知りたいのである。これは,今までの説明によって理解できるはずだ。知りたいのは
という平均のバラつき,つまり,
の標準誤差なのである。それでは,
の値はどこから得られるだろうか。
まずは,困難度,
を等化した後の差を見てみよう。その差は
となる。先ほど説明したように,
と
は推定値ではなく,真の値である。したがって,
が成り立っている。そうすると困難度の差は
となる。
つまり,表6.1で見た困難度の差は,となっていたのである。
これで,の標準誤差,すなわち
の標準偏差が計算できる。既に説明したように,あるデータセットに定数を加え合わせても,分散や標準偏差は変化しないからだ。
の標準誤差は
の標準誤差と同じである。
したがってLinking Errorの計算式は次のようになる。困難度の差の分散を,共通項目の問題数をnとすると,困難度の差の標準誤差は
となる。これがLinking Errorである。表6.1のデータを使うとPISA2000とPISA2003を等化する際のLinking Errorは
と計算される。つまり困難度の差の平均は0.041ロジット程度は平均的にバラつくということだ。すなわち,等化係数も0.041ロジット程度はバラつき,それに従いPISA2003の平均得点もまた0.041ロジット程度バラつくことになる。これは,平均得点の標準誤差と見なせるため,有意性検定の式にLinking Errorを加えるのである。
ただし,このままでは検定の式に代入することはできない。得られたLinking Errorはロジットスケールの値なので,これをPISAのスケールに変換しなければならない。PISA2000とPISA2003の場合,基準となるのはPISA2000のスケールであり,その標準偏差は100,平均は500となっている。
Linking Errorは標準誤差,つまり平均得点のバラつきなので平均が500という尺度を考慮する必要はない。標準偏差を100にするだけである。PISA2000の受験者能力の標準偏差は1.1002なので(OECD 2005 pp.214-215),PISAスケールに変化したLinking Errorは,
\begin{equation}
\cfrac{1}{1.1002}×0.041×100 \risingdotseq 3.727
\end{equation}
となる。なお,数字が丸められている分(か筆者が間違っているため)PISAの報告書とはわずかに違いがある。PISAでは3.744と報告されている。
*1:ところで,母平均が分かっている状況はそれほど多いわけではない。というよりも,それを知ることが調査の目的であることも多い。そこで,母平均
の代わりに標本平均
を代用することがある。しかしこの場合,分散(の期待値)は過小に評価されることがわかっている。そこで,標本平均
を使っても母平均の不偏推定量となるように,nではなくn-1で割る。これを不偏分散と呼ぶ。ただし,以下の説明では大規模な学力調査の場合を想定しているため,自由度は基本的に考慮しない。
*2:心理検査や学力調査では,標準検査を作成する作業のことや,尺度値の意味付けに関わる作業のことも標準化(norming) と呼ぶことがある。
*3:正確には,累積分布関数とは確率変数Xの確率密度関数においてとなるようなxの関数である。
*4:これを変数とみなせば2母数モデルとなる
*5:項目反応理論で要求されるのは,厳密な独立の仮定ではなく,ある潜在特性θを固定したとき,個々のテスト項目に対して独立に反応する「局所独立の仮定」である。つまり,IRTでは極めて強い(学力の)一次元性の仮定が置かれているといえる。
*6:{ここでは「データ」と表現しているが,これは必ずしも現実に観測されたデータを意味しているわけではない。たとえば,あるテストの得点が70点であったとき,これに対して「真の得点は80点である」という仮説を立てることができる。この場合,70点と80点というのがここでいう「二つのデータ」ということになる。



