以下の記事に触発されて書いた。「学力や偏差値とは無関係」としているが、学力と学習態度には少なからぬ関連があるためこの記事も多少は参考になると思う。ちなみに、大学生の質の変化を調べたものとしては既にベネッセの「大学生の学習・生活実態調査」があるため、本当に大学生の質的変化を議論したいのであればそちらを参照した方が良い。
Ⅰ.大学生の偏差値換算
少子化と大学進学率の上昇は誰もが知っている事実であり、この二つから導かれる帰結は大学生のレベル低下である。そこで、『学力低下は錯覚である』(神永, 2007, p.41)に記載されている偏差値換算式の説明をする。やっていることは単純なので統計学の知識はそれほど必要ではない。
換算式
ここでは換算したい年度の偏差値、
は基準となる年度の偏差値、
は
の年度と
の年度の人口比である(
)。ただし、大学の定員数は一定とする。この式の意味を出来るだけ直感的に説明する。
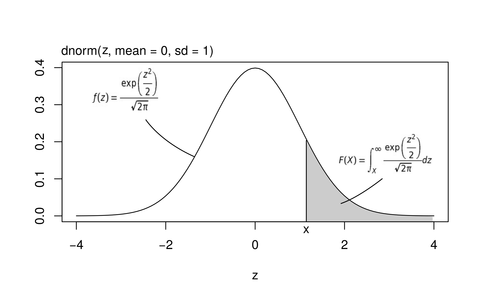
まずは左式F(X)を説明する。式中の関数は標準正規分布の確率密度関数と呼ばれるものであり、平たく言えば平均が0、標準偏差(バラつき)が1となるような正規分布の関数である。グラフにすると上図のように0を中心とした左右対称の曲線となる。それをXから∞まで積分するのがF(X)であり、上図の網掛けの部分の面積がそれである。なおF(X)の範囲は0~1となる。
次に右式を説明する。式中に関数Fが含まれているが、それに(x-50)/10という値が与えられている。ここで何をしているのかと言えば、換算したい偏差値xを標準化している。標準化というのはあるデータ(セット)を標準正規分布に従うデータ(セット)に変換する作業のことであり、たとえば、偏差値60を標準正規分布の尺度に変換すると(60-50)/10=1となる。これを上掲のグラフに当てはめると以下のようになる。
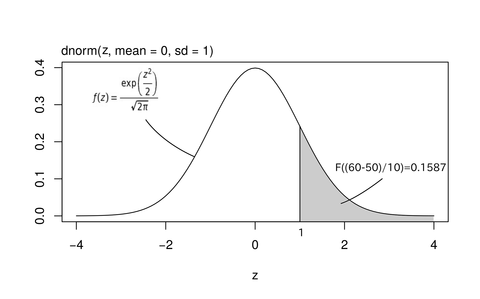
F(X)=0.1587となる。仮に学力が正規分布しているならば、偏差値60以上の人が16%存在するということである。ここで、上図を大学生の偏差値分布、網掛けの面積を人数と読み替え、さらに補助線として大学の総定員数aを導入する(aは最終的に消えるので何人でも良い)。そうすると、(ある世代集団の)大学生集団における偏差値60以上の人は0.16*a人いるということになる。たとえばa=500,000ならば、偏差値60以上の大学生は約8万人程いる計算になる。
世代人口を倍すると、当然ながら偏差値60以上の人口も
倍となり、0.16*al人となる。たとえば、x世代の人口が100万人、y世代の人口が200万人の場合を考える。このとき、x世代において偏差値60のAさんは自分より上に8万人いるが、y世代の人口に換算すると上に16万人いることになる。言い換えれば、人口が2倍になったことで上位8万位から16万位へ順位を落としたということである。
後は50万人中16万位という順位を偏差値に換算するだけである。これには関数Fの逆関数であるを使う。偏差値からその集団内における相対的順位を導くのが関数Fであったので、その逆関数
は相対的順位から偏差値を導くことができる。たとえば、50万人中16万人は上位32%に位置しているので、0.32を代入すると0.48が返ってくる。これを偏差値の形式に直すと偏差値55となる。x世代の偏差値60はy世代の人口を基準にすると偏差値55まで下がるということである。
以上の手順を簡単にまとめると次のようになる。
1.x世代の偏差値を標準化する(e.g.偏差値60→1)
2.関数Fを使い標準化得点から集団内の相対的位置を計算する(1→0.16)
3.これをy世代の人口を基準とした数値に換算する(0.16→0.32)
4.Fの逆関数を使い集団内の相対的位置から標準化得点を計算する(0.32→0.48)
5.標準化得点を偏差値の形式に変換する(0.48→55)
以下留意点を三つほど挙げておく。
①偏差値変化の幅は偏差値が低いほどに大きい
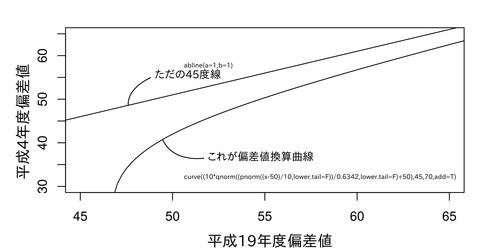
神永(2007)から。グラフにすれば明らかだがもう少し直感的に捉えてみる。今、100万人の集団Aがいるとする。次に、この100万人の集団から奇数番目の人を引っこ抜き、それを集団Bとする。集団Bでは隙間が目立つので前に詰める。集団Aで2位だった人は一歩前に進んで1位になる。4位だった人は2歩進んで2位になる。6位だった人は3歩進んで3位になる…といった具合に続き、最後に100万位だった人が50万歩進んで50万位となる。というわけで、学力が低い人間ほどその順位の変動は大きくなる。もちろん彼らの学力が変化したわけでもなく、集団Aと集団Bの平均学力は変わらない。
②偏差値差の大きさは学力差の大きさを意味しているわけではない
詳しく説明するとやや込み入った議論になるのでここでは簡単に示す。上掲のグラフを見れば分かる通り、偏差値換算曲線は偏差値50を切ったあたりから急激に低下している。これを神永は「マイナス無限大」「低すぎて見えない」と表現しているが、これは誤解を招きかねない表現である。偏差値46あたりでマイナス無限大になるのは確かだが、それ以下は無限大(inf)ではなく計算不能(NaN)になる。具体的に確認する。
> 10*qnorm((pnorm((47-50)/10,lower.tail=F))/0.6342,lower.tail=F)+50
[1] 30.51602
> 10*qnorm((pnorm((46-50)/10,lower.tail=F))/0.6342,lower.tail=F)+50
[1] NaN
警告メッセージ:
qnorm((pnorm((46 - 50)/10, lower.tail = F))/0.6342, lower.tail = F) で:
計算結果が NaN になりました
偏差値47を換算すると偏差値30強であったのが、偏差値46を換算した途端に計算不能となっている。もちろん、これは偏差値と47と偏差値46の間に隔絶した学力差が存在することを意味しているわけではない。上記の計算をより具体的に書けばこの原因が分かる。
> pnorm((46-50)/10,lower.tail=F)
[1] 0.6554217> (pnorm)((46-50)/10,lower.tail=F))/0.6342
[1] 1.033462
まずは偏差値46の上側確率を求める。結果は0.66であり、つまり上位2/3に位置しているということになる。これを人口比で割る、すなわち平成4年度の人口を基準とした数値に換算すると1.03となる。確率が1を超えるのだから当然に計算不能である。これが意味しているのは「平成19年度換算で偏差値46の大学生は、平成4年度換算では大学に入れない」ということである。偏差値46と偏差値47の間に存在するのは学力差ではなく大学定員の壁である。
以上の例からも分かる通り、偏差値の差から(我々が実感する)学力の差は導けない。一方の集団で計算すると偏差値が1しか違わないにも関わらず、一方の集団で計算すると30以上も違ってしまう、ということが起こりうるからである。①で示したように、学力の低い人ほど人口変動の影響が大きいのは確かだが、換算された偏差値差をそのまま学力差として解釈することはできない。結局の所、偏差値という概念は正に偏差値という概念として理解するしかないのであり、これを学力という類似の概念で説明しようとすることに誤解の原因がある。
③大学生の学力と大学生世代の学力は異なるものである
これまでの記述から必然的に導ける結論だがあえて強調するだけの重要性はある。単純な例を考えてみる。今、学力水準がほぼ同じ二つの集団A,Bがあるとする。ただし、集団Bの方が僅かに学力が高い。学力水準は同じでもその人数は異なり、Aが200万人、Bが100万人である。ここで、大学の定員を50万人とする。そうすると、集団Aでは上位25%の人が大学へ進学する一方、集団Bでは上位50%の人が大学へ進学できる。そうすると次のような事態が起きうる。
まず、大学生の平均学力が低下する。集団Aでは上位25%しか大学へ進学できなかったのが、集団Bでは上位50%まで大学へ進学できるからである。また、各大学の定員が変わらないとすれば、この学力低下は個々の大学でも起こる。そして(こちらは忘れられがちなのだが)、大学へ進学しなかった層の学力も低下する。集団Aでは下位75%が非進学者であったのに対し、集団Bでは下位50%しか残っていないからである。
この状況はシンプソンのパラドックスと呼ばれる。全てのサブグループの平均得点が低下(向上)しているにも関わらず、グループ全体の平均得点は向上(低下)する現象のことである。現象とは言っても数学的には当然であり、その数理も難しいものではない。卑近な例を挙げれば野球の打率である。たとえば、二人の選手A,Bが2018-2019シーズンに記録した打率を、2018:.400(A), .350(B), 2019:.285(A), .280(B)とする。いずれのシーズンもA>Bとなっているが、 二つのシーズンを合計した打率はどちらが上か分からない。打数が分からないからである。
恐らく、野球ファンであるならばA>Bと即断することはない。野球ファンならば打率という指標がそれほど頑健ではないこと、打数によっては上下に大きく変動することを感覚的に知っているからであり、仮に打率が.400に届こうものならまずは打数の少なさを疑うはずである。故にシンプソンのパラドックスを回避することができる。対して、大学進学率の上昇による必然的な学力低下が殆ど考慮されないのは、「大学生」や「高卒」といった属性が一個の人格的イメージを伴って実体視されているからかもしれない。なるほど二人しかいなければパラドックスは生じないはずである。
SATスコアの急落―危機に立つ国家
少し話は逸れるが、アメリカでもシンプソンのパラドックスが学校教育の混乱を招いた事例がある。1983年にアメリカのレーガン政権が作成した"A Nation at Risk"という報告書に見られた事例である。”危機に立つ国家”の邦訳でも知られるこの報告書は知っている人も多いかもしれない。その詳細な内容はGoogleに任せるが、簡単に言えばいかに現代アメリカの学校教育が糞であるかを力説したものであり、その何よりの根拠がSATスコアの急落であった。
アメリカ政府はこの甚大な学力低下をさらに詳細かつ充実した形で文書化するため、サンディア国立研究所にレポートの作成を委託したのだが、研究者達の引き出した結論は逆であった。つまり、彼らは近年のアメリカの教育について、"驚いたことに、ほぼすべての指標で安定的な、或いは僅かな改善傾向を示すことを見出した"のであり、問題とされたSATスコアの低下については"SATの平均得点が60年代から低下しているのは事実だが、その原因は学生のパフォーマンスではなく、従来の受験者に加えて成績下位層もSATを受験するようになった結果"であり、"全てのサブグループの平均得点が向上してもなお全体の平均得点が低下しうる現象は「シンプソンのパラドックス」と呼ばれる”と結論付けた。(https://www.jstor.org/stable/20404979?seq=1)
面白いことに、その後のSATでは(見かけ上)これとは逆の現象も生じている。高校生の各グレードの平均得点が減少しているのに対し、SATスコアの全体平均は向上していたのである。
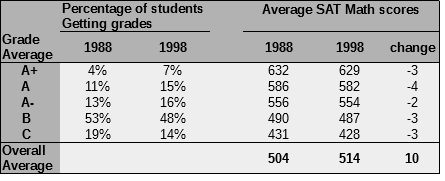
表を見れば明らかな通り、このような変化が生じたのは下位グレードから上位グレードへの流入が起こったためである。結果として全てのグレードレベルでは平均得点が低下しているものの、全体平均では10ポイントの向上を示している。ちなみにこの表の出典は1998年9月2日付の"The New York Times"の記事であり、論調としては最近の高校はグレードがインフレしていてけしからん的なものだったらしい。
Ⅱ.出席率の変化
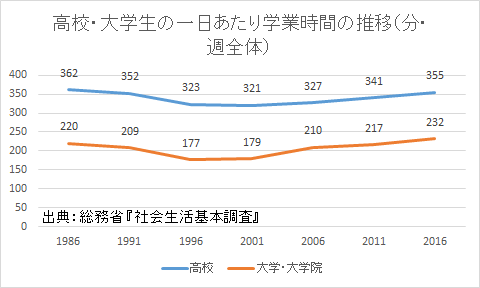
この20年間で大学生の平均学業時間は一日当たり50分以上伸びており、恐らくその主因は"大学の学校化"による学生の出席率の増加である。だとすれば、近年の大学生が消極的に見えるのは、正にそうした学生が大学に顔を見せるようになったことが原因であり、翻って"大学のレジャーランド化"と呼ばれていた時代にはそもそも消極的な層が文字通り見えなかったのではないかという仮説。後で書く。書かないかもしれない。
結語
本当はこうした記事を書かない方が良いのかもしれない。本来ならそれが大学教員であろうと誰であろうと「単なる実感に意味は無い」と言ってしまえば済む話である(少なくとも面接試験に反対する教員は自分の実感を一切持ち出さないでほしい)。それがこうした記事を書くことで、その実感にある種のお墨付きを与えてしまっているような気がしてならない。